On Randomness (and Parity)

Reprising the last post on tactics and dice rolls and then a deep dive into what Randomness .. is(?)

I read back through the last post about football tactics and dice rolls, and I thought of some ways to clarify/summarize it, so that might be helpful.

But also, since the last post, we have seen the rebirth of the blogger Michael Caley (as opposed to the podcaster) by way of his new Newsletter: Expecting Goals. In the spirit of a nerdy soccer blogging renaissance, the kind of which John Muller and I at Post Script Podcast encourage (part of the reason for trying to document nerdy soccer blogging origins in audio discussion form), it feels appropriate that Caley had some poignant thoughts on Randomness that I wanted to link to and engage with and then see how it sits with the way I’ve been thinking about randomness in articles like the last one.

Recent Recap

First, clarifying/summarizing the basic idea in the last post:

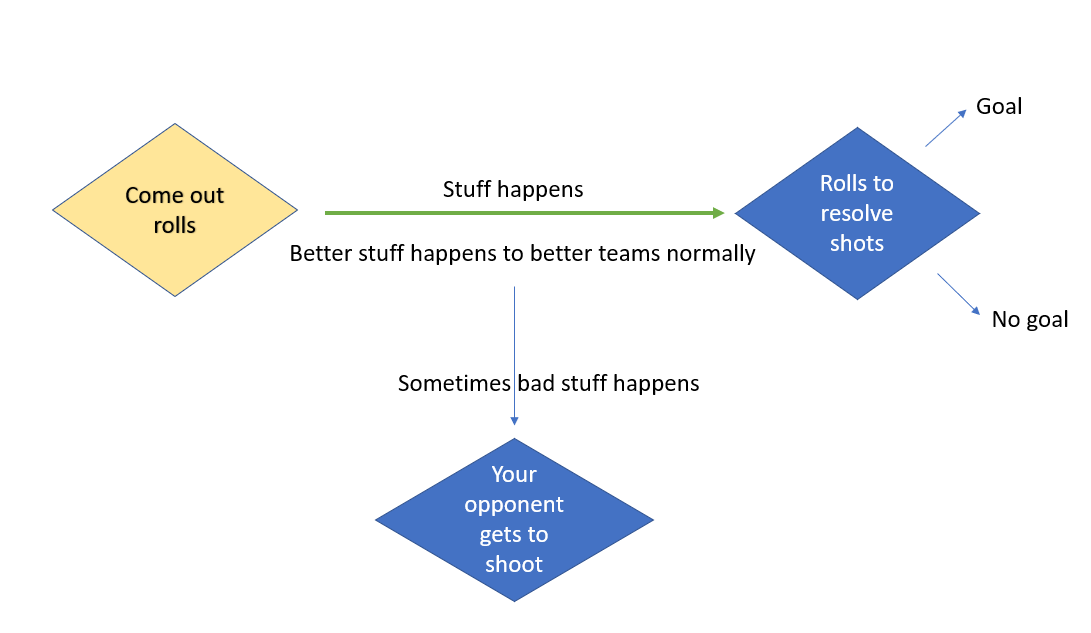
This was a bad powerpoint graphic I haphazardly threw together after I had published the post. Come-out rolls (I will push forward and take some risk, I might get a good attacking chance, or leave myself vulnerable to a counter) are like minor dice rolls that you choose to roll or not roll. If you roll them and then do some soccer, it may or may not lead to big dice rolls (I will shoot, I might get a goal or miss and give them a goal kick). If your come-out roll comes good, you’re more likely than normal to find a shot (big dice roll), if it fails, you’re more likely than you would otherwise be to give up a dangerous counter attack (this is the attacking version of it at least).

The basic thing is that as a starting point, some stuff is going to happen in the game no matter what. Both sides are trying to score and not get scored on broadly speaking and the players have free will and different abilities and then because the ball is round and you can’t hold it, it’s gonna bounce around weird and random stuff will happen interacting with those different abilities (and discrepancies in abilities) and intentions. When something does happen, you might even get a shot on the end of it. And those shots that sometimes happen after stuff happens are important because sometimes they go in AND sometimes they don’t. And they fluctuate in their going-in-ed-ness and they’re miss-ed-ness in wild ways over small sample sizes like football matches. So basically, in all matches, some shots are going to happen and whether or not those shots are goals is a function of both a) how open and near and footed those shots are (i.e. whether it’s a “good” chance) and b) randomness (and also c - finishing skill which is small and frankly boring).

How much Stuff happens however (and therefore indirectly how many shots might then happen in the game), is partly to be determined by the risk appetites of the two teams. Games can happen where neither team really wants to risk anything and open up, and you end up with the Simpsons soccer meme (very few shots). “Holds it!”

Other games happen where the managers appear to have entered into some kind of death pact with each other and their teams just viciously charge forward and attack back and forth on the break with no semblance of structure or risk management or defense to be found (lots of shots). Rest defense is for losers they whisper to themselves at full sprint.

Importantly, if we then take an example where a really strong team is playing a really weak team, then the fewer the shots there are in the game (adjusted for xG), the more likely it is that the randomness attached to any one shot (and all the shots together) is going to make the result of the match seem weird compared to the relative strengths of those two teams. Said another way, when a strong team plays a weak team and not much stuff happens, randomness is more likely to overcome the disparity in team strengths than when lots of stuff happens (cuz stuff happening is kinda what we think of as soccer). So it follows that strong teams would rather have the death pact type matches with weak teams where lots of stuff happens rather than Simpsons meme matches where nothing happens.

And that’s just sort of a weird paradoxical thing to think about. A lot of times strong teams want to “control the match” in ways that they think are to their advantage (they might think “my enemy is variance, so let’s eliminate it”). But if you ascribe to this framework, it’s just weird, like to mitigate variance you should take on risk. You should do the opposite of “control the game” maybe.

On Randomness

So there’s that, the weird finding that I think is worth thinking about, and then there’s the second thing, which is that if you ascribe to the first thing, then this is a really big part of a manager’s job actually: the management of risk appetite to right-size it depending on who his team is playing. And another way to say “the management of risk appetite” is to say the “thinking about randomness and then desiring a certain amount of it (directionally) as part of the actual tactics your team uses in the game.” That is to say, randomness is a thing the coach (or whoever) actively thinks about, and this is where I wanna talk about chance and “Analytics.” Which is something Caley briefly did in his introductory newsletter recently.

Finally there is randomness. Sports analytics does not merely attribute outcomes to bad luck but seeks to quantify that variation to understand how, when and to what degree it impacts sporting outcomes and achievements. When someone says that a player who is not finishing their chances right now likely will not remain cold, this is a statement about randomness. The sample size over which the statistical record has been compiled is too small to draw conclusions about the real underlying skill of the player or team that compiled those statistics. The holy grail of the study of randomness is projectibility. Can you say based on a player’s record what their likely statistical production will be over the next several weeks, months or years? What parts of the statistical record, over what sample sizes, provide useful signal to identify those underlying real tendencies and capabilities?

So I don’t disagree with him here. And for context, he was defining “soccer analytics” and laying out sort of three broad aspects of it, which maybe I’ll paraphrase as:

1. Valuation - how do we put a value on soccer stuff, everything from players to actions to tactics as measured in something like win probability or goals or something like that (if you’re reading Absolute Unit, I bet you’re familiar)

2. Context - because statistics are just abstract recordings of rich, complex things that actually happen in real life, how do we make sure we don’t mess up our analysis when we look at these rather flattened statistics. How do we adjust or filter statistics in such a way so as to ensure they reflect real life stuff as much as they can, or in ways that are useful to us, or at the very least not misleading to us.

3. Randomness - that above block quote, basically randomness gets in the way of using statistics at their face value to understand soccer because of characteristics of probability. Similar to how we can’t just take flattened statistics at their word because of differing contexts, we also can’t trust them unless we have an adequate enough sample size because of their tendency in many cases to regress toward a mean (and away from any one given observation).

To ponder randomness the way Caley does above (which is critical) is to think about… OK stay with me here as we throw on our annoying grad school hats, the epistemology of soccer. So, like philosophy has these couple branches:

Ontology - what is there? and

Epistemology - how do we know?

So Caley’s (and I would say almost all actionable, useful) analysis of randomness in sport considers it as a barrier to the pursuit of knowledge. So it goes that we have this amazing game called soccer, and we’re trying to understand it better with statistics, but there’s these epistemological barriers due to the nature of statistics: the flattening of context, and the randomness that doesn’t resolve itself unless we have really large sample sizes, and often the largeness required here extends beyond several seasons worth of data.

And I think something that interests me about randomness in soccer is that not only is it a barrier to understanding soccer through statistics — something we strive to overcome through sound methodology (an aspect of analytics). But it’s more than that. It’s also part and parcel to, or an inherent characteristic of Soccer (something that really pops out when you contrast it with other sports). It’s something that managers are or should be aware of and impacts their decision making (in ways that are perhaps more intimate than how a Director of Analytics or a Sporting Director would).

Randomness is Soccer’s Soul

Randomness is baked in by design in soccer — it is a critical part of how the game is experienced, recorded, accounted for, scored, etc. And a team’s interactions with randomness (or its preference for a certain level or amount of randomness over some other amount) directly influences how the game is played and what the outcomes are on the pitch (and then indirectly, also what those recorded outcomes are as statistics).

Randomness is not just a phenomenon of recorded statistics, a veil we must pierce to better understand soccer through numbers. It’s thing that can be felt I think. Every sport experiences some degree of randomness. In fact, my favorite quote from Carlin Wing makes the claim that this is what separates Games from Sport:

A ball introduces a second, more uncertain, kind of uncertainty into the fray. Its bounce dances along the edge of our predictive capacity, always almost but never fully under control. At least in the Anglophone world, this second kind of chance—the chance of the ball—seems to be especially important to our contemporary understanding of play.² While other kinds of contests are raced, run, rowed, and swum; wrestled, fenced, fought, and boxed; timed, weighed, measured, and judged; ball games are played. And only an athlete who contends with balls (or pucks, or shuttlecocks, or other third objects) earns the title “player.” We become players in and through bounce.

Every game though has rules, and a lot of what these rules do is they attempt to tame the inherent randomness that is inserted by the ball. What makes soccer beautifully different from these other sports is that by design, the rules (laws and structure) of soccer do very little (if anything) to counteract this randomness. For anyone who grew up focusing on other sports and not soccer, it’s shocking. It’s hard for me to put it into words — it just feels like, the only sport that wasn’t born into (or yet ruined by) super annoying arguments about fairness made by dudes who love to argue about stuff. It almost didn’t occur to *gestures broadly* .. soccer that randomness was even undesirable.

So it got me thinking about the characteristics of randomness, or the characteristics of sports that influence how significant the effect of randomness is on the experience. I was thinking of posting one of the all time worst radar charts but the groupchat threatened me with violence, so here’s a table. These are what I might call attributes that influence randomness. Red means more randomness and green means less (these numbers scaled 1-100 are placeholders based on judgment and not measured. We can quibble about these estimates if you like. Measuring these would be cool!

I break up these randomness attributes into the physical, the accounting, the structural, the interdependence, and league regulations.

The reference point of randomness has to involve the scoring. Basically when we say a sport has a high degree of randomness, we’re firstly talking top-down about how random the results are, and the results are the outputs of a specific kind of accounting: scoring. When we talk about “how random” the results are, I think it’s easy to mix up two different things, but they’re often hard to parse. You might have noticed how I separated the above graphic into two separate tables. On my view, one factor that influences how random we perceive the results to be isn’t really about randomness, it’s about parity: the actual quality gap between teams that are competing. You could have a contest between competitors of exactly the same ability level, and if the accounting allowed for ties or draws, a perfectly non-random sport would return all draws. Even though there’s no clear winner in this league, we wouldn’t say that it’s random. It’s very predictable. If the sport had a modest level of inherent randomness, but had perfect parity among its competitors, then the results would be very hard to predict. This sport would appear to be very random, in part because its competitors have equal ability, and it’s hard to measure significant real differences between them but we would observe significant real differences in results due to randomness. You would need a pretty long season for the records of all the teams to converge together. By contrast you can have teams with marginal differences between them in ability, but if they play a perfectly non-random sport, those marginal differences will cement themselves in the scores and in the results fast enough such that the sport is not considered random at all. So that’s why I separate randomness from parity. These are two different attributes that interact in interesting ways to make results predictable or not. Sometimes we see the combination of these things labelled as some kind of measure of randomness. This inclination is understandable.

Anyhow, when we focus not on parity, but on inherent randomness (bounce?), we can talk about these characteristics of a sport/game:

The Accounting

• How frequent are scoring plays? In general the less frequent the scoring plays are, the more random the results of matches are because there isn’t an adequate sample size of recorded scoring actions to confirm that the better team won the game. Contrast an NBA game with a soccer match.

• Do scoring plays have to pass some final specific gate or hurdle, i.e. a dedicated goal defender — a goalkeeper? Since, the frequency of scoring moments has a major impact on the randomness of the sport, whether these scoring moments have additional random conditions attached to them also matters. If a team can perform well and move the ball or puck into a great shooting situation, only to be foiled by an otherworldly save by a goalkeeper ( a goalkeeper who could just as easily not save that shot on another day), we could say that the team’s results are more random. This is similar to the “frequency of scoring plays” factor above.

  • Special shoutout to basketball. If soccer has a big old dice roll every time there’s a shot, basketball basically has this every time a shot misses, because while shooting is definitely a differentiating skill in basketball, where the misses end up (offensive rebound, defensive rebound) is more impacted by bounce/variance (I think).

If abstract scoring is the reference point around which randomness orbits, the foundations of its effects are instead physical in nature. And because the scoreline is the reference, we’ll orient these effects based on the offensive team:

The Physical

• How much control of the ball/puck does the offensive team have? In general, when you can hold the ball with your hands and use your feet to run, whatever happens next is more predictable and can be more often linked with progressing the ball toward a scoring moment with some consistency. If the ball is constantly taking funny bounces, and turnovers abound — say if you have to control the ball with the same thing you use to move your body — then randomness is higher. If as an offensive player you have to strike a ball hurtling toward you at 96 miles per hour with a narrow stick and then where it goes specifically in front of you is really important in determining whether you progress to first base (toward a scoring action), then randomness is higher. If you can hold the ball and your progression forward is largely a function of whether your teammates successfully blocked (or otherwise foiled) the defense, that’s less random.

• How “successful” is the most common offensive play or action at progressing the ball towards a scoring moment? If the most common offensive play is that a batter swings and misses, or that he is otherwise retired by the pitcher without progressing to first base (toward a scoring moment), we can think of this as a more randomized basic nature of play. This is again similar to the frequency of scoring factor. Basically, when failure of a given offensive play is the most likely outcome, there is a real randomness to what’s going to happen next and a weaker connection between player ability and whether a sequence of plays creates a score.

Then there’s characteristics of randomness that have to do with the underlying structure of play, play basically being the offense attempting to progress the ball towards a scoring moment and the defense trying to stop it. These characteristics could be summarized as:

The Structural

• How repetitive and uniform is the nature of the tasks/actions that make up play? Is an offensive player tasked with similar actions each play. Is he repeating the same pitcher vs batter duel each at bat? Is he lining up most every play with the goal of pushing back the same defensive lineman in front of him? Or does he find his role and his focus and his objectives changing drastically minute to minute based on something that has just happened? More uniform actions give us a bigger sample size of a similar contest that might help us measure towards a scoring event. Less uniformity in action just means that whatever has happened in the past may not look like what will happen in the future. We’re just sort of always starved for adequate data to predict the future.

• How frequent is play broken up into dead ball resets. The question of whether a player is facing similar situations over and over again is in large part a question of whether there are “resets” which automatically bring play back to these similar starting situations or not. Baseball and American football are games of repeated deadball resets. Basketball is more fluid but in general the players find themselves in similar starting situations for the majority of the plays (there are fast breaks and scrambles for sure, but there is also a steady shot clock which does a lot to divide play up into discrete possessions). Deadball resets are good experiments for determining whether the better team will win than fluid play with more variables.

• When play is not stopped, what is the degree to which players return to similar positions between plays? See the basketball example above. Play is fluid between most basketball possessions, even when a team scores, they don’t blow the whistle and set offside lines. Instead, play keeps moving. Still, the nature of the sport is that on most plays, players end up in similar situations based on their position. Centers and forwards closer to goal, guards more likely around the perimeter, basic shapes or structures from which they rotate and move around trying to score. In hockey, possessions flow into one another, but you can basically count on seeing two defensemen hanging back while three forwards take up positions closer to goal. The more likely for players to face similar scenarios each play, the less random the sport is, the more likely it is that we can just kinda add up measures of these similar scenarios and find signal that might align with results.

• How discrete and/or protected is the progress of the ball toward a scoring moment by the offensive team? In American Football if a quarterback throws a 15 yard pass and the receiver drops it, whatever progress the offense has made up to that point is not lost entirely. It is protected in this way, play is reset back to the line of scrimmage and the offense still has 2 more downs to gain 10 yards and keep progressing the ball. And if they approach running out of downs, they can boot the ball away forcing the opponent to start deep in their own territory. In soccer, an incomplete pass, normally means an immediate turnover and sprinting back the other direction. Less protection of previous ball progression = more randomness. Baseball is in the middle here. The offense has the protection of sending another batter out there when the first one strikes out, but after three outs any progress they’ve made around the bases is wiped clean and the ball turned over to the other team to attempt to score. A less random version of baseball would be one team batting until it reaches 27 outs, then the other team batting until it reaches 27 outs. Instead we have the more random structure of the game. The faceting of individual at bats into uniform plays adds to consistency, but the separation of play into discrete innings at the three out marker adds randomness because of the lost progress: the stranded runners. When progression is protected/discrete/faceted, then scoring is more likely to reflect a team’s sustained ability to progress the ball. When progression resets continuously and in varying ways, it’s more likely that stuff that happens is not going to align with team strength and long term results.

When more than one sovereign will has to cooperate in order for an offensive team to succeed, variance in the outcomes of the results will be higher.

The Interdependent

• To what degree can we attribute the success of individual ball progressing plays to individuals versus to the team as a whole? In general, in the face of an inherent physical randomness due to a lack of control, if a sport involves having to get multiple people on the same page with each other in order to advance the offense, you’re going to have a higher degree of disfunction. When it comes to collaborating and getting on the same page, defense and disruption is just easier than coordination and creativity. So the result is just more turnovers, less protected progression of the ball (see above). Whatever other inherent randomness was there, it just gets exacerbated a bit when the sport requires close coordination of multiple participants.

And finally, are there any decisions the major sporting leagues have made to mitigate or amplify the underlying randomness of the games themselves?

The Regulatory

• How many games are included in the regular season? In general, the longer the season the less random the regular season results are. Baseball has some incredibly random inherent attributes; however, the league plays 162 games so that at some point during that season, the randomness washes away, and they’re able to determine with some confidence, who the best team is (or the best few). By contrast, the NFL (a much less inherently random game), adds a bunch of randomness to its season results, by only having the teams play 17 regular season games (as well as an unbalanced schedule).

Conclusion

I’ve long wanted to inventory and describe these various factors so thanks for indulging me. I think there’s a lot of useful and actionable insights that can come from a more careful exploration of this — done by someone better at it than myself.

• From a league-wide business perspective, if you’re a small growing league, or a large, growing league, or maybe you’re trying to build a Super League :(, or you’re worried you might have to pick up the pieces after one, or you’re thinking about new formatting for your postseason or a structuring a new knockout tournament, I believe carefully considering the interactions between these various characteristics of randomness and parity can really inform your analysis and assist in better outcomes.

• Specifically if you’re Major League Soccer and you find yourself at this very intriguing node of randomness/parity where parity is significant in overall terms (even if you’re not perfectly capped like the NFL) and randomness is sky high because it’s soccer, and let’s say you’ve been trying to grow your business by looking to examples from wildly profitable and popular sports like the NFL, I think it is CRITICAL to examine the differences in randomness/parity between these two sports before trying to map over one success to another. The downside risk to not performing this analysis seems significant to me. My worry is that for the inherent level of randomness in soccer (something you can’t really change), the decided upon level of parity (a policy choice) is still set too high such that the result is incoherent narratives and matchups without any real dramatic stakes. Forget about those who demand pro/rel. I’m not talking about those kind of stakes, I’m just saying narrative stakes that build enjoyment. Which team is good? How good? Are they supposed to win? Should I watch this because they’re a likely champion? The other team is not good. Oooooh but wait, are they still level at halftime? That’s interesting. Maybe I can catch an upset! vs “anything can happen in MLS and most teams are similar in quality but all equally unlikely of being champion.”

• But if you’re a manager and you’re thinking through tactics, again I want to emphasize that a part of your job needs to be recognizing the optimal alignment between risk taking and variance/randomness as it relates to your relative parity with other teams in the league (or in individual matchups you’re preparing for). Importantly, this is a neutral impact to your team’s let’s call it expected performance in a given game. You may be the special manager who can squeeze an extra 5% of performance out of your squad via man-management or your special game model, but I’m starting to believe the larger impact you can have is helping to control the range of outcomes in your team’s individual matches (around a neutral expected level of performance), so that over the course of a season as you play better teams and worse teams and similar teams, results are more likely to fall in line with the front office’s expectations.

• If you write about soccer, I think understanding some of these interactions between chance, parity, etc really helps to get clarity in your own head about what are compelling narratives or ideas for articles and what aren’t. Or if there are parts of this you want to emphasize in some cases and not in others.

Appendix: Influence — Old Blog Posts on Parity

I want to acknowledge an influence here. This “randomness index” I tried to imagine in this post, as far as I can trace it in my brain is at least partially influenced by a “parity index” I came across trolling through some old blog posts from 2010. User sidereal at the old SounderAtHeart blog wrote a 4 part series on parity. In the first one he introduces what he calls “Three Kinds of Parity.” There’s “franchise parity” which is how quickly a team can bounce back from being bad in one year and be good in the next year (or vice versa). There’s “Season Parity” or how tightly grouped the final standings are such that either the final table or the final postseason participants are not solidified until late (when there’s high season parity) or vice versa (when there’s low season parity). And finally there’s “game parity” which is how likely is it for an underdog to defeat a strong favorite in any one game. He ironically calls this “any given Sunday” parity.

The author assigns “franchise parity” (bounce-backedness) largely to the bylaws and front office mechanics of a given league, which makes sense. He attributes “Season Parity” to the mechanics of the seasonal structure of the league, more focused on how many teams make the playoffs, and what kind of brackets there are, how many divisions, wildcards etc. I think this is compelling, though I would overlay that largely speaking salary cap impacts this as well (offset by something else below). He then attributes” game parity to the underlying laws of the game/sport basically. Identifying the random nature of striking a fast ball with a small bat as something inherent in the laws of baseball. Game parity is then to be managed he would assert by extending the season or postseason such that enough games can pass such that the game to game parity can even itself out and good teams can succeed.

I love this framework and if I were to emphasize/adjust part of it I would just reiterate that “game parity” is largely a function of something like 1. talent disparity, 2. inherent randomness, and 3. home advantage.

I would describe season parity as largely a function 1. talent disparity (reduce this down to cap/spending rules), 2. individual game disparity, and 3. season structure (how many games etc).

Franchise disparity for me would then be a function of 1. Season disparity (how much a given season’s results hadn’t regressed much to its mean), 2. league rules around drafts/free agency and 3. broadly speaking player labor power (unionized or otherwise, how effectively can free agents force moves or demand higher salaries etc such that they’re constantly ending up on teams with cap money to spend who might have had bad years etc)